Explicando a produtividade marginal dos fatores de produção

Introdução

É bem comum se deparar com manuais de teoria econômica ou com estudos econômicos aplicados que utilizam a derivada da função de produção como uma medida para a produtividade marginal dos fatores de produção. No entanto, o mais correto seria tratar esta derivada como sendo o produto marginal dos fatores, o qual informa a variação marginal do produto dada uma variação marginal no fator de produção específico. Usando este mesmo conceito, a produtividade marginal de um fator de produção deve esboçar o quanto a produtividade total muda marginalmente em decorrência de uma alteração marginal no uso deste fator de produção. Neste breve post, busco mostrar de maneira didática uma alternativa factível para a produtividade marginal dos fatores.

Detalhes da tecnologia de produção

Considere um produtor representativo racional que produz um produto \(Y\) usando apenas dois fatores de produção, o capital \((K)\) e o trabalho \((L)\). Suponha que este produtor opera de acordo com uma tecnologia de produção do tipo Cobb-Douglas, tal que:

\[Y= K^\alpha L^{1-\alpha}\]

Em que \(0\leq \alpha \leq 1\) é o parâmetro de compartilhamento da tecnoologia de produção que expressa a participação do capital nos custos.

Modelando a produtividade

Para um fator de produção específico, a sua produtividade pode ser expressa como a quantidade de produto decorrente unicamente do uso deste fator. Em termos formais, a produtividade de um insumo pode ser medida como a razão entre o produto total e a quantidade utilizada deste insumo. No caso deste esboço, a produtividade do capital \((\delta_k)\) pode ser expressa como:

\[\delta_k = \frac{Y}{K}\] \[\delta_k = \frac{K^\alpha L^{1-\alpha}}{K}\] \[\delta_k = \left(\frac{L}{K}\right)^{1-\alpha}\] A produtividade do trabalho \((\delta_L)\), por sua vez, pode ser escrita como:

\[\delta_L = \frac{Y}{L}\] \[\delta_L = \frac{K^\alpha L^{1-\alpha}}{L}\] \[\delta_L = \left(\frac{K}{L}\right)^{\alpha}\]

A produtividade total dos fatores de produção \((\delta)\) é a soma da produtividade individual de cada fator. Portanto:

\[\delta = \delta_k+\delta_L\] \[\delta = \left(\frac{L}{K}\right)^{1-\alpha}+ \left(\frac{K}{L}\right)^{\alpha}\] \[\delta = \left(\frac{L}{K}\right)\left(\frac{K}{L}\right)^{\alpha} + \left(\frac{K}{L}\right)^{\alpha}\] \[\delta = \left(\frac{K}{L}\right)^{\alpha}\left[\frac{L}{K} +1\right]\] \[\delta = \left(\frac{K}{L}\right)^{\alpha}\left[\frac{L+K}{K}\right]\]

A produtividade marginal do capital

Para encontrar uma medida para a produtividade marginal do capital, basta derivar a produtividade total dos fatores em relação ao insumo capital, obtendo:

\[ \frac{\partial \delta}{\partial K} = PmgK = \alpha K^{\alpha -1}\left(\frac{1}{L}\right)^{\alpha}\left[\frac{L+K}{K}\right] + \left(\frac{K}{L}\right)^\alpha \left[\frac{K-(L+K)}{K^2}\right]\\ PmgK = \alpha\left(\frac{1}{K}\right)\left(\frac{K}{L}\right)^\alpha\left[\frac{L+K}{K}\right] -L \left(\frac{1}{K}\right)^2\left(\frac{K}{L}\right)^\alpha\\ PmgK = \alpha\left(\frac{1}{K}\right)^2\left(\frac{K}{L}\right)^\alpha\left[L+K\right] -L \left(\frac{1}{K}\right)^2\left(\frac{K}{L}\right)^\alpha\\ PmgK = \alpha\left(\frac{1}{K}\right)^2\left(\frac{K}{L}\right)^\alpha\left[L+K-L\right]\\ PmgK = \alpha\left(\frac{1}{K}\right)^2\left(\frac{K}{L}\right)^\alpha K\\ PmgK = \alpha\left(\frac{1}{K}\right)\left(\frac{K}{L}\right)^\alpha\\ PmgK = \alpha\left(\frac{1}{K}\right)^{1-\alpha}\left(\frac{1}{L}\right)^\alpha \] Note que \(PmgK \neq \frac{\partial Y}{\partial K}\). Porém, note que \(PmgK = \frac{\partial Y}{\partial K}/L\), uma vez que:

\[ \frac{\partial Y}{\partial K} = \alpha K^{\alpha -1}L^{1-\alpha}\\ \frac{\partial Y}{\partial K} = \alpha\left(\frac{1}{K}\right)^{1-\alpha}L^{1-\alpha}\\ \frac{\partial Y}{\partial K} \left/ \right. L = \frac{\alpha\left(\frac{1}{K}\right)^{1-\alpha}L^{1-\alpha}}{L}\\ \frac{\partial Y}{\partial K} \left/ \right. L = \alpha\left(\frac{1}{K}\right)^{1-\alpha}L^{-\alpha}\\ \frac{\partial Y}{\partial K} \left/ \right. L = \alpha\left(\frac{1}{K}\right)^{1-\alpha}\left(\frac{1}{L}\right)^{\alpha}\\ \]

Note que a produtividade marginal do capital cai sempre que há um aumento na quantidade de insumos utilizadas no processo de produção.

A produtividade marginal do trabalho

Para encontrar uma medida para a produtividade marginal do trabalho, basta derivar a produtividade total dos fatores em relação ao insumo trabalho, obtendo:

\[ \frac{\partial \delta}{\partial L} = PmgL = \alpha \left(\frac{K}{L}\right)^{\alpha -1}\left(\frac{-K}{L^2}\right)\left[\frac{L+K}{K}\right] + \left(\frac{K}{L}\right)^\alpha \left[\frac{K}{K^2}\right]\\ PmgL = \left(\frac{K}{L}\right)^\alpha \left[\frac{1}{K}\right] - \alpha \left(\frac{K}{L}\right)^{\alpha -1}\left(\frac{1}{L^2}\right)\left[L+K\right]\\ PmgL = \left(\frac{K}{L}\right)^\alpha \left[\frac{1}{K}\right]- \alpha \left(\frac{K}{L}\right)^{\alpha} \left(\frac{L}{K}\right)\left(\frac{1}{L^2}\right)\left[L+K\right]\\ PmgL = \left(\frac{K}{L}\right)^\alpha \left[\frac{1}{K}\right]- \alpha \left(\frac{K}{L}\right)^{\alpha} \left(\frac{1}{K}\right)\left(\frac{1}{L}\right)\left[L+K\right]\\ PmgL = \left(\frac{K}{L}\right)^\alpha \left[\frac{1}{K}\right]\left[1- \frac{\alpha(L+K)}{L}\right]\\ PmgL = \left(\frac{K}{L}\right)^\alpha \left[\frac{1}{K}\right]\left[\frac{L-\alpha(L+K)}{L}\right]\\ PmgL = \left(\frac{K}{L}\right)^\alpha \left[\frac{1}{K}\right]\left[\frac{L(1-\alpha)-\alpha K}{L}\right]\\ PmgL = \left(\frac{1}{L}\right)^{\alpha+1} \left[\frac{1}{K}\right]^{1-\alpha}\left[L(1-\alpha)-\alpha K\right] \] Note que \(PmgL \neq \frac{\partial Y}{\partial L}\). Note também que neste caso \(\frac{\partial Y }{\partial L}/K \neq PmgL\), indicando que tomar a derivada da função de produção e em seguida tomar a razão entre o resultado e a quantidade utilizada dos demais insumos nem sempre é uma boa aproximação para a produtividade marginal do fator de produção.

Visualização da produtividade marginal dos fatores

Para representar graficamente a produtividade marginal do capital, considere um caso fictício em que \(\alpha = 0.5\) e suponha um horizonte de curto prazo com o insumo trabalho fixo em \(L= \bar{L} = 50\).

pmgk = function(a, k, l){
  return(
    a*((1/k)**(1-a))*((1/l)**a)
  )
}


K = c()

for(i in 1:100){
  K[i] = pmgk(a = 0.5, k = i, l = 50)
}


ggplot() +
  geom_line(aes(x = 1:100, y = K), col = "blue", size = 1.1)+
  theme_bw()+
  ylab("Produtividade marginal do capital") + 
  xlab("Total utilizado do insumo capital")
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## i Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

Para representar graficamente a produtividade marginal do trabalho, considere o mesmo caso fictício denotado para a produtividade marginal do capital.

pmgL = function(a, k, l){
  return(
    ((1/l)**(a+1))*((1/k)**(1-a))*(l*(1-a) - a*k)
  )
}


L = c()

for(i in 1:100){
  L[i] = pmgL(a = 0.5, k = i, l = 50)
}


ggplot() +
  geom_line(aes(x = 1:100, y = L), col = "blue", size = 1.1)+
  theme_bw()+
  ylab("Produtividade marginal do trabalho") + 
  xlab("Total utilizado do insumo capital")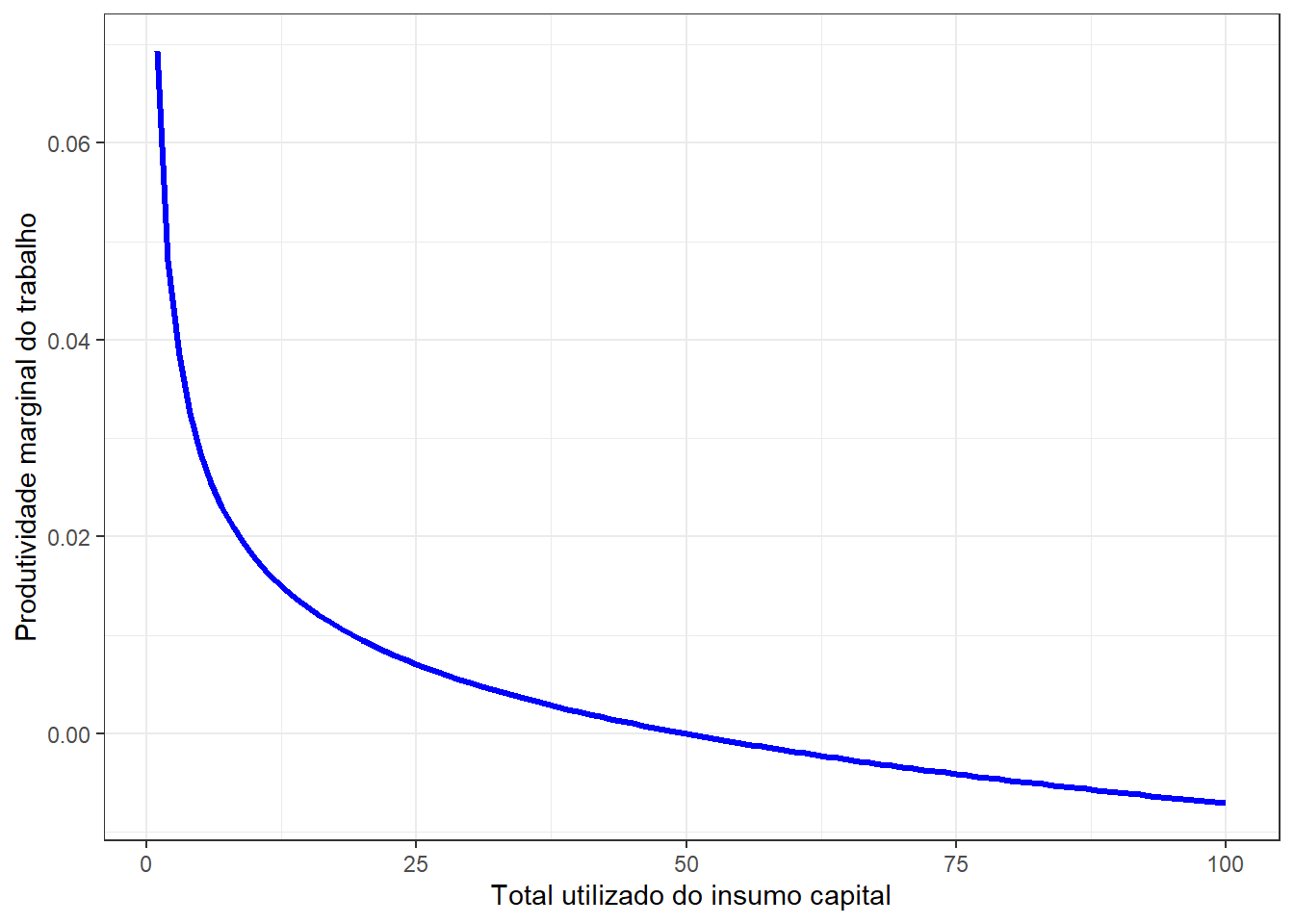

Conclusão

Utilizar a derivada da função de produção como medida para a produtividade marginal do fator de produção pode retornar um valor superestimado para a verdadeira produtividade marginal dos fatores dado que produto marginal é um conceito diferente de produtividade marginal.