Alpha C. Chiang. Elements Of Dynamic Optimization. 1992: Respostas do Capítulo 7 em R

March 14, 2025

$\text{ }$

Exemplo 1, página 171.

\[ \max \; V = \int_0^T - (1-u^2)^{1/2} dt\\ \text{Sujeito a:}\\ \dot{y} = u\\ y(0) = A\\y(T) \text{ livre}\\ \text{$A$, e $T$ dados} \]

O primeiro passo para a resolução do problema é instalar as bibliotecas necessárias e liberá-las para o uso. De início, considere usar a biblioteca deSolve, ideal para a resolução de equações diferenciais.

lapply(list("deSolve"), function(x){
  if(x %in% installed.packages() == F){
    install.packages(x)
    require(x, character.only = T)
  }else{
    require(x, character.only = T)
  }
})
FALSE Carregando pacotes exigidos: deSolve
FALSE [[1]]
FALSE [1] TRUE

Feito isso, o próximo passo é resolver o problema. Como $A$ e $T$ são dados, considere $A=1$ e $T=4$ para viabilizar a resolução.

# Parâmetros
T <- 4 # Tempo final
lambda <- 0.5 # Valor arbitrário para lambda

# Função de controle
u <- function(lambda) {
  lambda / sqrt(1 - lambda^2)
}

# Equação diferencial
dy_dt <- function(t, y, params) {
  list(u(params$lambda))
}

# Condição inicial
y0 <- 1

# Tempos
times <- seq(0, T, by = 0.01)

# Resolvendo a EDO
out <- ode(y = y0, times = times, func = dy_dt, parms = list(lambda = lambda))


# Plotando resultados
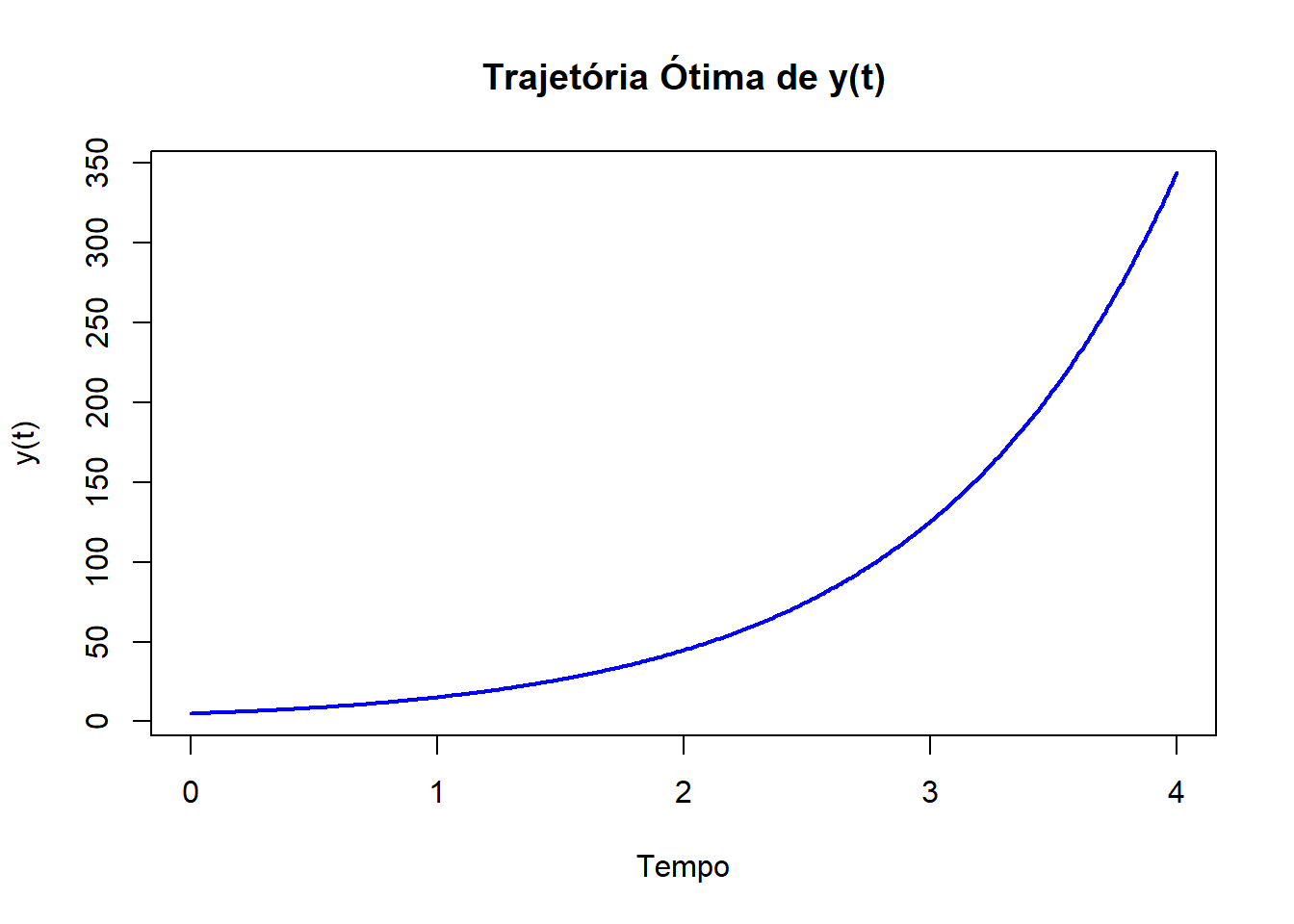
plot(out, xlab = "Tempo", col = "blue", lwd = 2, ylab = "y(t)", main = "Solução y(t)")
grid()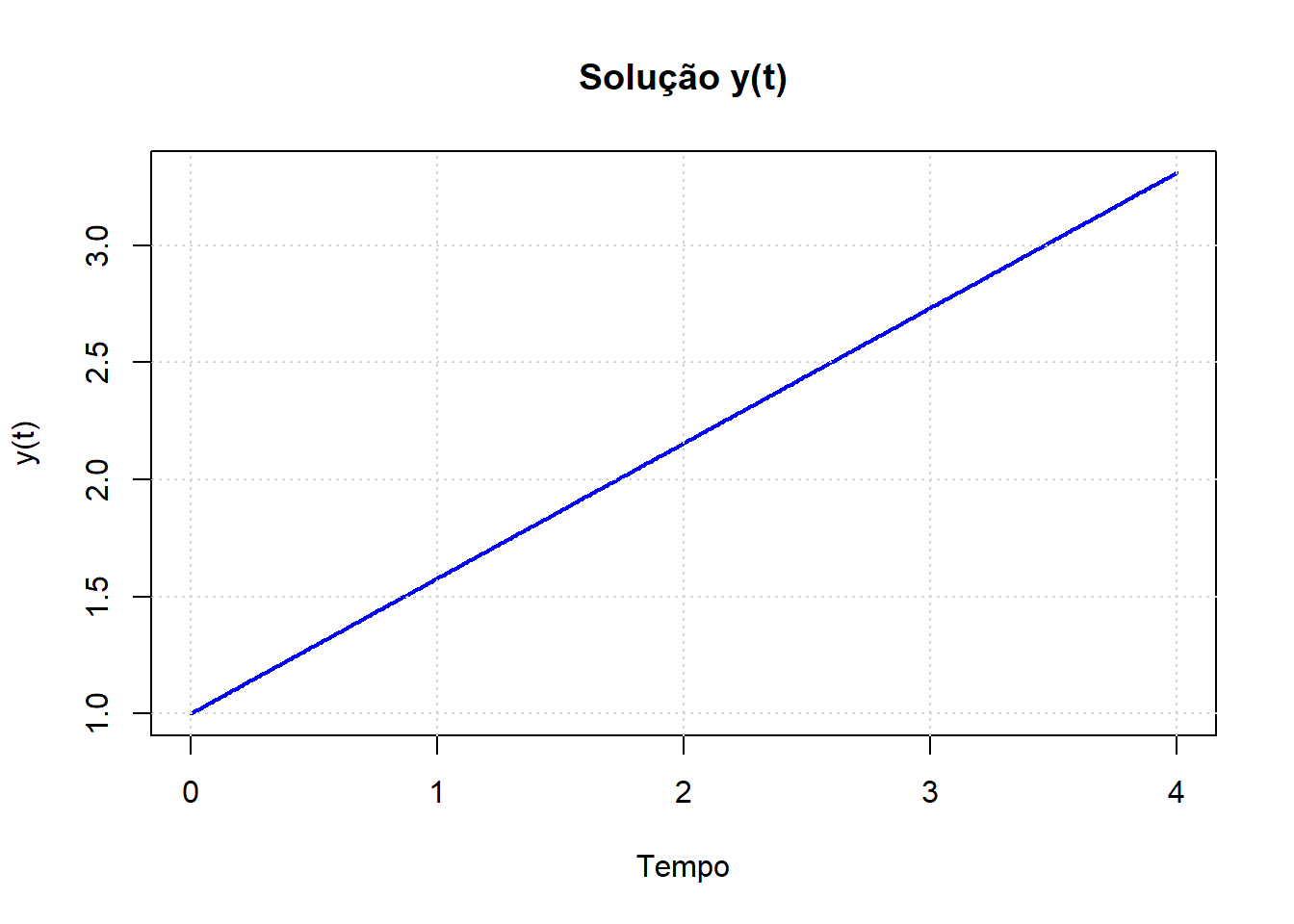

Exemplo 2, página 173.

\[ \max \; V = \int_0^2 (2y - 3u) dt\\ \text{Sujeito a:}\\ \dot{y} = y+u\\ y(0) = 4\\y(2) \text{ livre}\\ u(t) \in [0,2] \]


# Função do sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo
  u <- max(0, min(2, (3/1) * lambda))
  
  # Derivadas
  dy <- y + u
  dlambda <- -2 - lambda
  
  list(c(dy, dlambda))
}

# Condições iniciais
state <- c(y = 4, lambda = 0)  # Supondo lambda(2) = 0
time <- seq(0, 2, by = 0.01)

# Resolver o sistema
results <- data.frame(ode(y = state, times = time, func = dynamics, parms = NULL))

# Plotar os resultados
plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória Ótima de y(t)")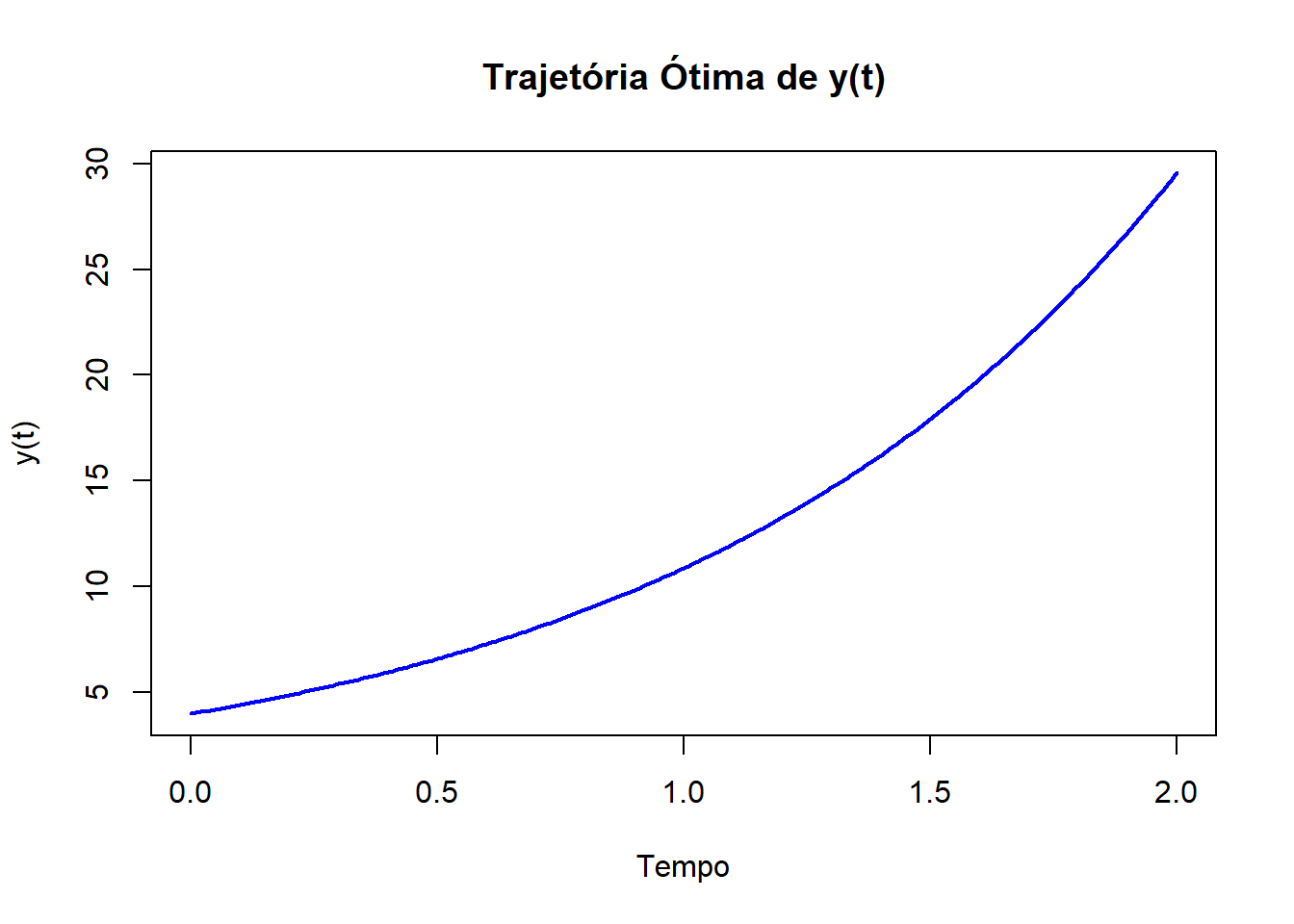

Exercício 7.2: Questão 2, página 176

\[ \max \; V = \int_0^4 3y dt\\ \text{Sujeito a:}\\ \dot{y} = y+u\\ y(0) = 5\\y(4) \text{ livre}\\ u(t) \in [0,2] \]

# Função que define o sistema de equações diferenciais
# Função que define o sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo
  u <- max(0, min(2, -lambda))  # Ajuste de u dentro do intervalo [0, 2]
  
  # Derivadas
  dy <- y + u
  dlambda <- -3 - lambda
  
  list(c(dy, dlambda))
}

# Condições iniciais
state <- c(y = 5, lambda = 0)  # y(0) = 5
time <- seq(0, 4, by = 0.01)   # Integração no tempo direto

# Resolver o sistema
results <- ode(y = state, times = time, func = dynamics, parms = NULL)

# Plotar os resultados
results <- as.data.frame(results)
plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória Ótima de y(t)")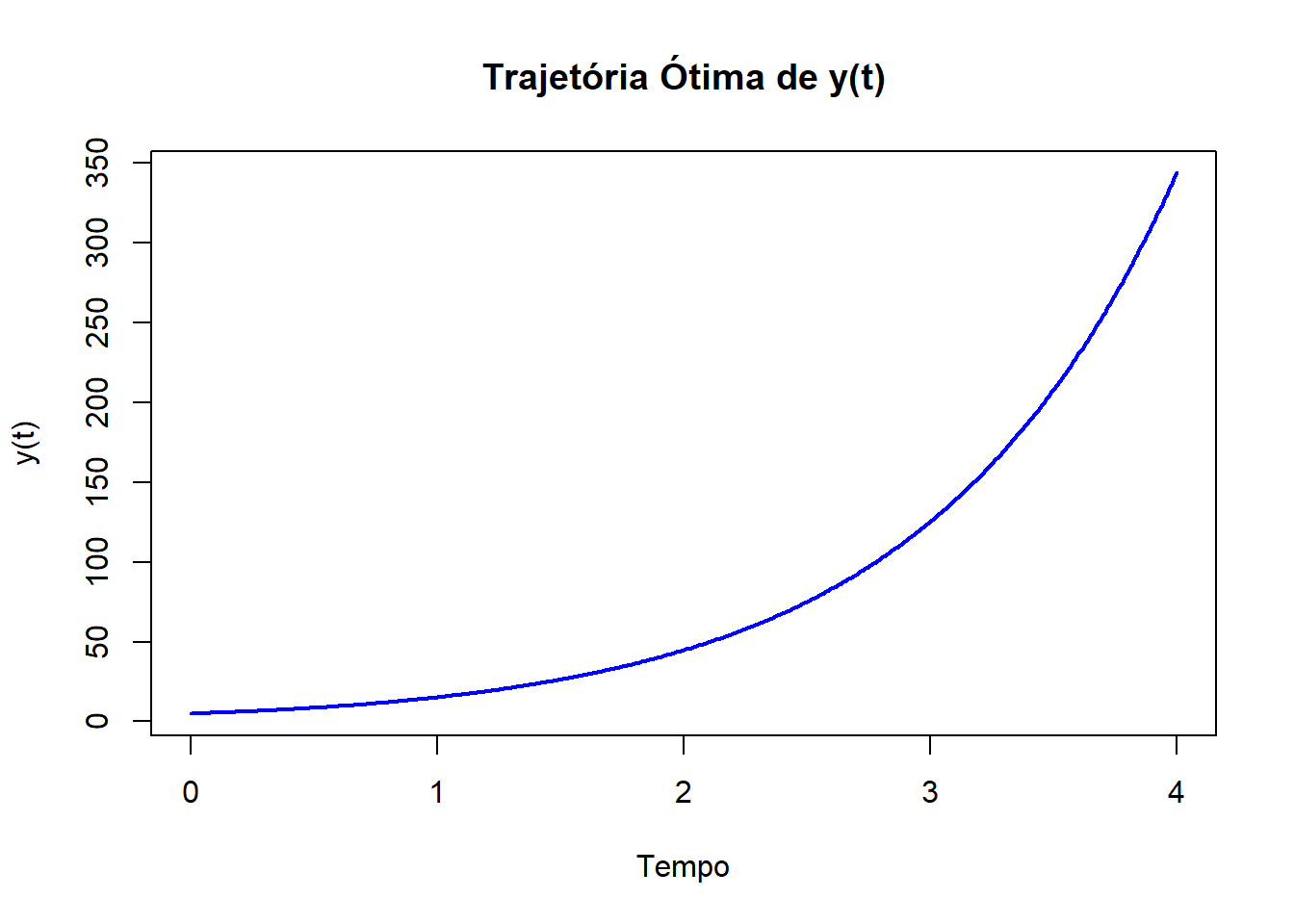

Exercício 7.2: Questão 3, página 176

\[ \max \; V = \int_0^2(y - u^2) dt\\ \text{Sujeito a:}\\ \dot{y} = u\\ y(0) = 0\\ u(t) \text{ irrestrito} \]

# Função do sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo
  u <- lambda / 2  # u não possui restrições
  
  # Derivadas
  dy <- u
  dlambda <- -1
  
  list(c(dy, dlambda))
}

# Condições iniciais
state <- c(y = 0, lambda = 0)  # y(0) = 0, λ final será ajustado (integração reversa possível)
time <- seq(0, 2, by = 0.01)

# Resolver o sistema
results <- ode(y = state, times = time, func = dynamics, parms = NULL)

# Plotar os resultados
results <- as.data.frame(results)
u_values <- results$lambda / 2

plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória Ótima de y(t)")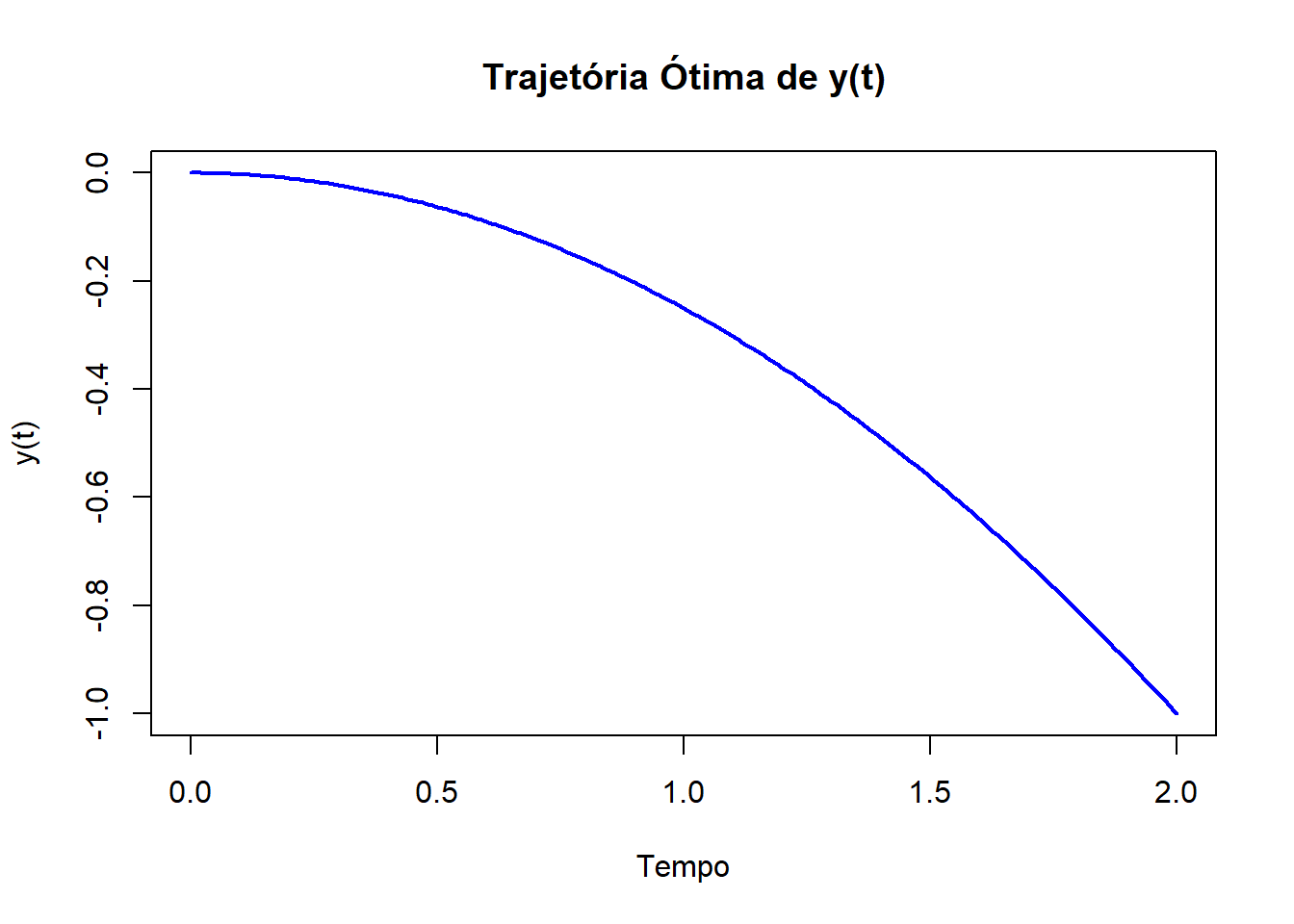

Exercício 7.2: Questão 4, página 177

\[ \max \; \int_0^1 -\frac{1}{2}(y^2 + u^2) dt\\ \text{Sujeito a:}\\ \dot{y} = u - y\\ y(0) = 1\\ u(t) \text{ irrestrito} \]

library(deSolve)

# Função que define o sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo
  u <- lambda  # Condição de máximo: u = λ
  
  # Derivadas
  dy <- u - y
  dlambda <- y - lambda
  
  list(c(dy, dlambda))
}

# Condições iniciais
state <- c(y = 1, lambda = 0)  # Condição inicial: y(0) = 1
time <- seq(0, 1, by = 0.01)

# Resolver o sistema
results <- ode(y = state, times = time, func = dynamics, parms = NULL)

# Plotar os resultados
results <- as.data.frame(results)

plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória Ótima de y(t)")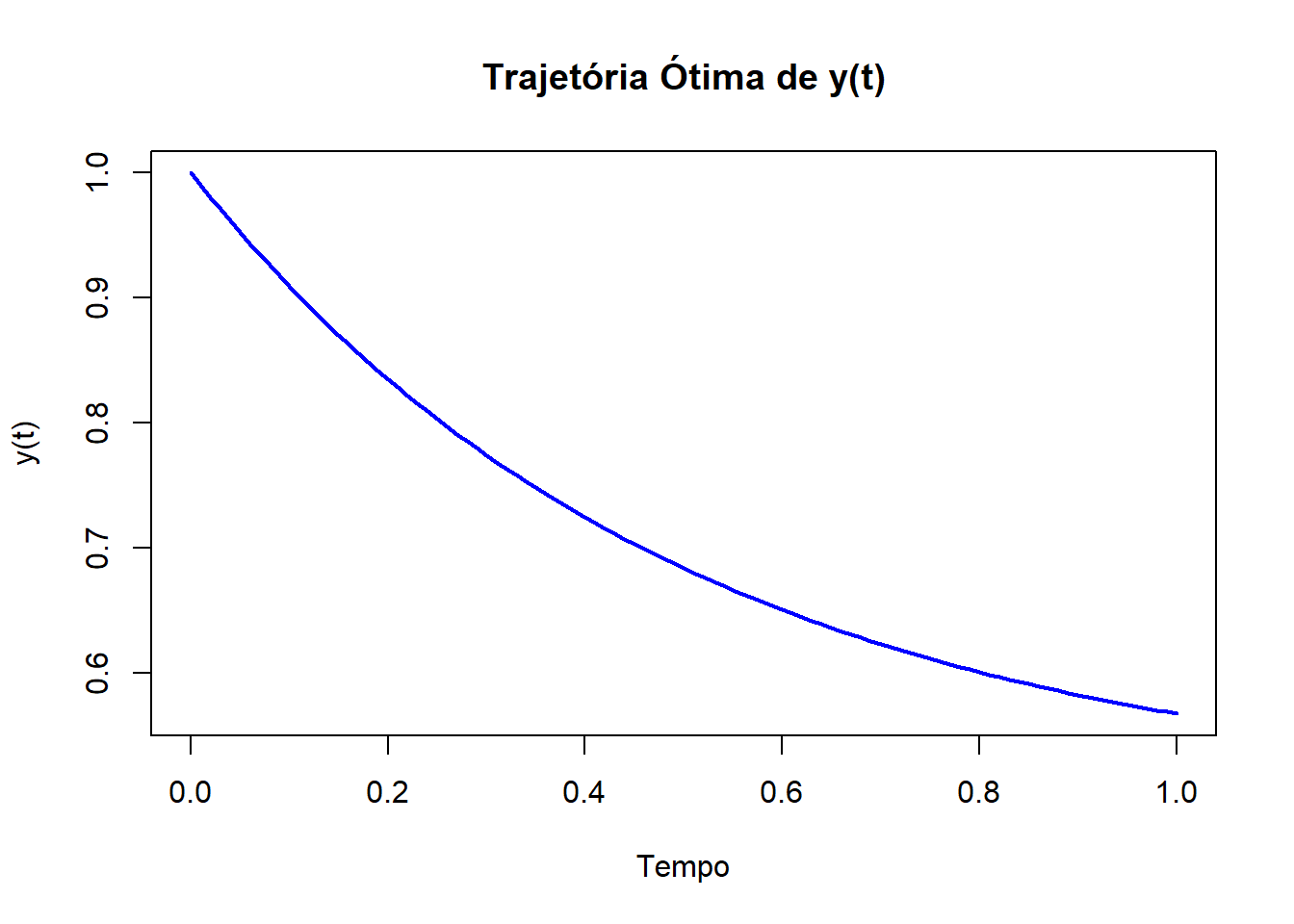

Exemplo 1: página 184

\[ \max \; V = \int_0^1 - u^2 dt\\ \text{Sujeito a:}\\ \dot{y} = y + u\\ y(0) = 1\\ y(1) = 0 \]

# Função para o sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo
  u <- lambda / 2
  
  # Derivadas
  dy <- y + u
  dlambda <- -lambda
  
  list(c(dy, dlambda))
}

# Condições iniciais e finais
state <- c(y = 1, lambda = 0)  # y(0) = 1; ajuste inicial para lambda
time <- seq(0, 1, by = 0.01)

# Resolver o sistema
results <- ode(y = state, times = time, func = dynamics, parms = NULL)

# Processar resultados
results <- as.data.frame(results)
plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória Ótima de y(t)")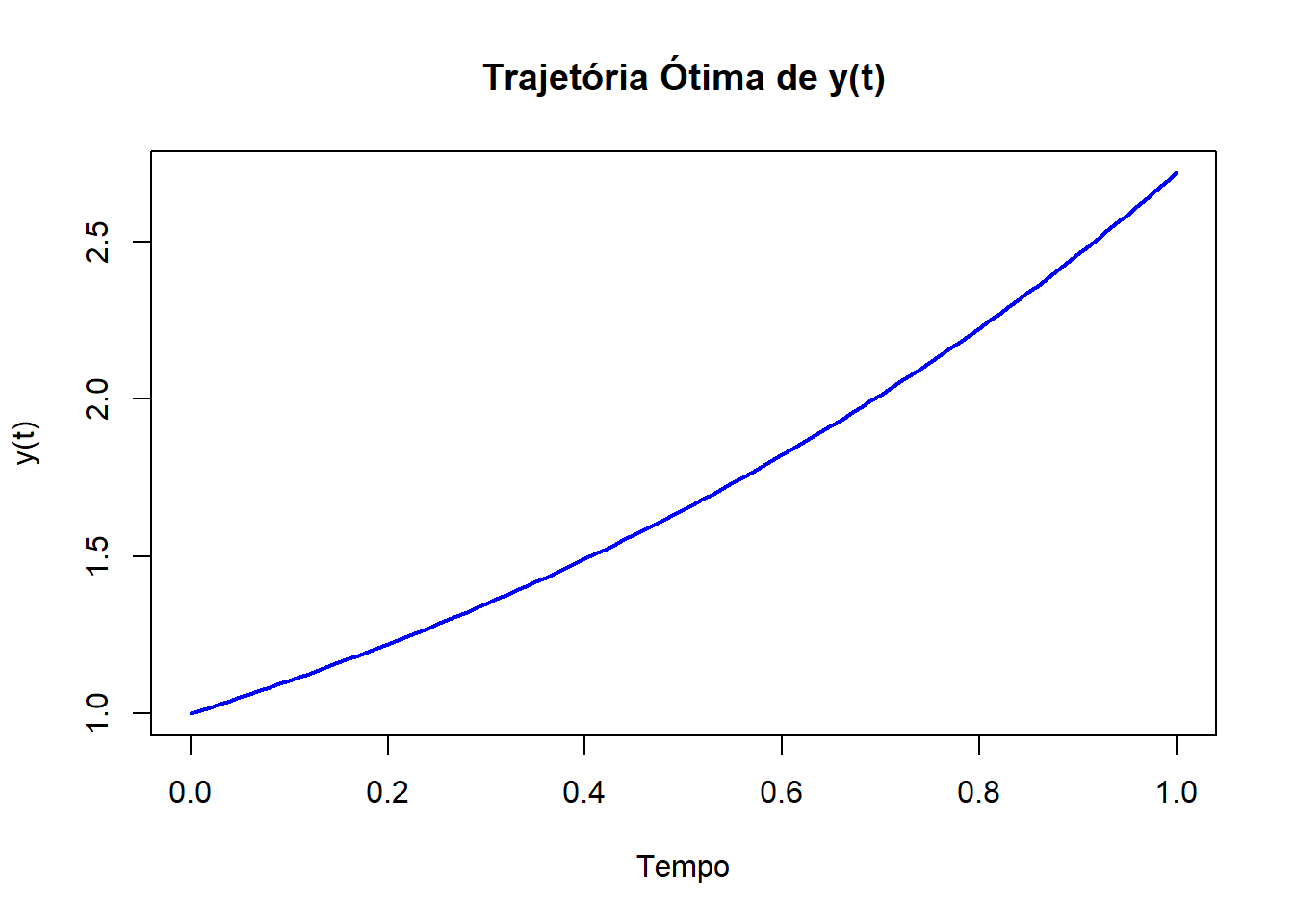

Exemplo 3: página 187

\[ \max \; V = \int_0^T - 1 dt\\ \text{Sujeito a:}\\ \dot{y} = y + u\\ y(0) = 5\\ y(T) = 11\\ T \text{ Livre} \\ u(t) \in [-1,1] \]


# Função que define o sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo baseado no sinal de lambda
  u <- ifelse(lambda > 0, -1, 1)
  
  # Derivadas
  dy <- y + u
  dlambda <- -lambda
  
  list(c(dy, dlambda))
}

# Parâmetros e condições iniciais
state <- c(y = 5, lambda = 0.1)  # Ajuste inicial para lambda
time <- seq(0, 10, by = 0.01)    # T estimado inicialmente

# Resolver o sistema
results <- ode(y = state, times = time, func = dynamics, parms = NULL)

# Processar os resultados
results <- as.data.frame(results)

# Plotar as soluções
plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória ótima de y(t)")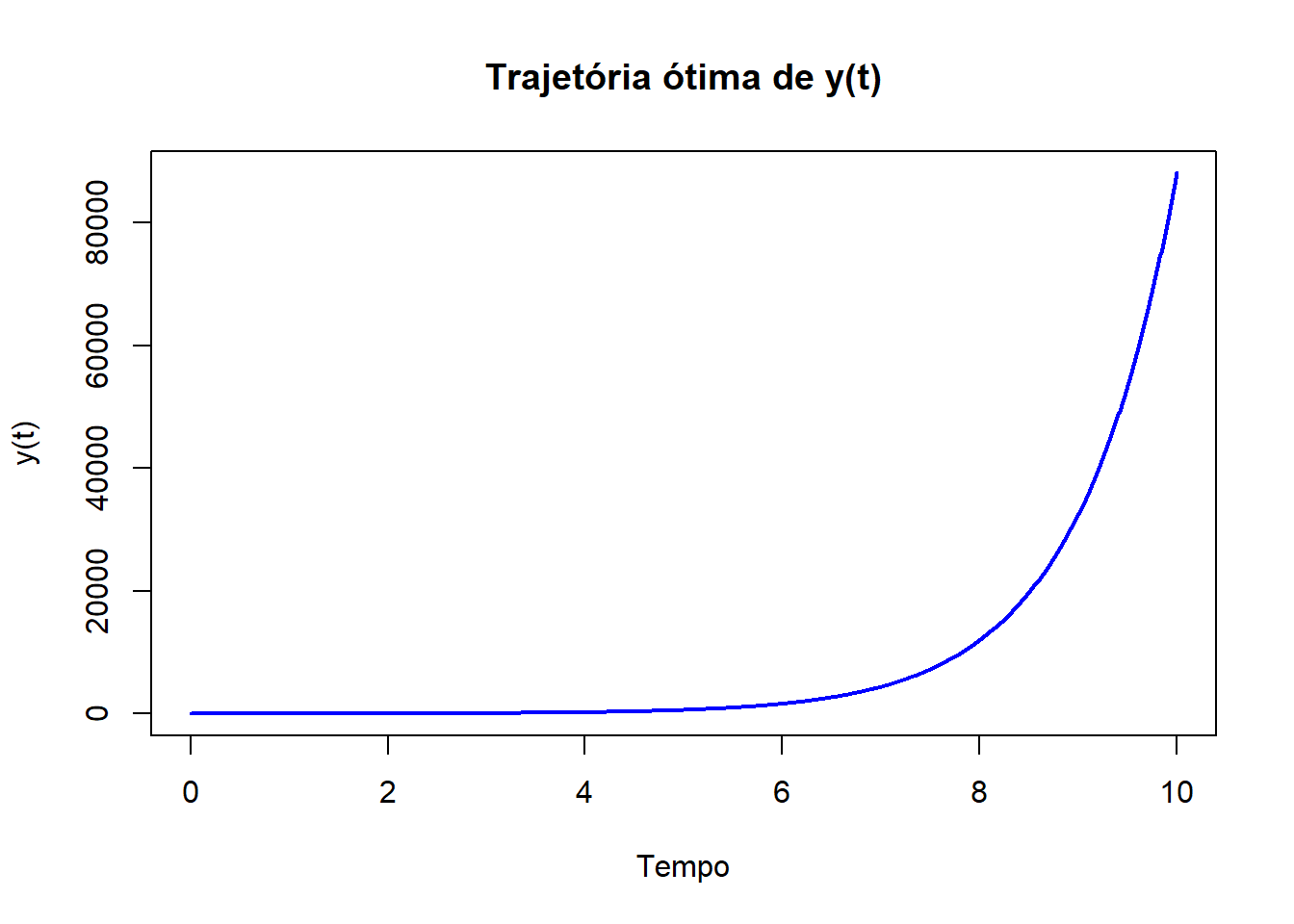

Exercício 7.4: Questão 1, página 191

\[ V = \int_0^T -(t^2+u^2) dt\\ \text{Sujeito a:}\\ \dot{y} = u\\ y( 0) = 4\\ y(T) = 5\\ T \text{ Livre} \]

# Função para o sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo
  u <- lambda / 2
  
  # Derivadas
  dy <- u
  dlambda <- 0  # λ é constante
  
  list(c(dy, dlambda))
}

# Função objetivo para ajustar T
objective_function <- function(T_guess) {
  # Tempo estimado
  time <- seq(0, T_guess, by = 0.01)
  
  # Condições iniciais
  state <- c(y = 4, lambda = 1)  # Suposição inicial para λ
  
  # Resolver o sistema
  results <- ode(y = state, times = time, func = dynamics, parms = NULL)
  results <- as.data.frame(results)
  
  # Erro entre y(T) e o valor-alvo (5)
  final_y <- tail(results$y, 1)
  return(abs(final_y - 5))  # Queremos minimizar esse erro
}

# Otimizar o tempo T para satisfazer y(T) = 5
optimized_T <- optimize(objective_function, interval = c(0.1, 10))$minimum

# Resolver com o tempo otimizado
time <- seq(0, optimized_T, by = 0.01)
state <- c(y = 4, lambda = 1)
results <- ode(y = state, times = time, func = dynamics, parms = NULL)
results <- as.data.frame(results)

plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória ótima de y(t)")

Exercício 7.4: Questão 2, página 191

\[ V = \int_0^4 3y dt\\ \text{Sujeito a:}\\ \dot{y} = y+u\\ y( 0) = 5\\ y(4) >= 300\\ u \in [0,2] \]

# Função que define o sistema de equações diferenciais
dynamics <- function(t, state, parameters) {
  y <- state[1]
  lambda <- state[2]
  
  # Controle ótimo (ajustado com restrição u ∈ [0, 2])
  u <- max(0, min(2, -lambda))
  
  # Derivadas
  dy <- y + u
  dlambda <- -3 - lambda
  
  list(c(dy, dlambda))
}

# Condições iniciais e finais
state <- c(y = 5, lambda = 0)  # Estado inicial
time <- seq(0, 4, by = 0.01)

# Resolver o sistema usando 'ode'
results <- data.frame(ode(y = state, times = time, func = dynamics, parms = NULL))


# Garantir que y(T) ≥ 300
if (tail(results$y, 1) < 300) {
  stop("Condição final y(4) ≥ 300 não foi atingida. Ajuste os parâmetros.")
}

# Plotar as soluções
plot(results$time, results$y, type = "l", col = "blue", lwd = 2, xlab = "Tempo", ylab = "y(t)", main = "Trajetória Ótima de y(t)")