Introdução à otimização de portfólio em R
Introdução
O objetivo principal do investidor é obter o máximo retorno com o mínimo risco. Neste âmbito, a otimização de portfólio surge como uma teoria que permite que o investidor aloque eficientemente os seus recursos com base nos seus níveis de aversão e aceitação do risco. Basicamente, esta teoria está fundamentada no pressuposto de que a diversificção da carteira é o passo básico para a minimização do risco e que a participação dos ativos de maior risco deve ser ponderada na carteira de investimento de acordo com as suas respectivas relações risco-retorno.
O modelo de Markowitz
O modelo de Markowitz é uma ferramenta que permite calcular o risco de uma carteira de investimentos, independentemente do tipo de ativos que a compõem. O objetivo do modelo de Markowitz, é possibilitar que os investidores que não gostam de riscos, possam construir uma carteira de investimentos com maior potencial de rentabilidade, a partir de determinado nível de risco de mercado. A ideia central da teoria é a construção de fronteiras eficientes em carteiras otimizadas, levando em consideração que o risco e o retorno precisam ser avaliados em conjunto dentro da carteira.
De maneira generalizada, o modelo de Markowitz retorna um conjunto de combinações possíveis de ativos, representados como pontos no gráfico, cujo eixo X corresponde ao risco e o Y é o retorno. Os pontos no gráfico formam uma curva hiperbólica ascendente, que reflete a fronteira mais eficiente possível. Desse modo, o investidor pode identificar qual a combinação de ativos que é capaz de produzir o resultado mais eficiente.
Escolhendo a carteira ótima
Para demonstrar a aliação do modelo de Markowitz, suponha que queiramos identificar o peso de cada ativo em uma carteira composta por ações das empresas Suzano, Vale, Telefônica e Marfrig. O primeiro passo é liberar as bibliotecas necessárias para a elaboração da carteira ótima.
lapply(list('BatchGetSymbols', 'tidyverse', 'ggplot2', 'fPortfolio'), function(x){
if(x %in% installed.packages() == FALSE){
install.packages(x)
require(x, character.only = TRUE)
}else{
require(x, character.only = TRUE)
}
})
## Carregando pacotes exigidos: BatchGetSymbols
## Carregando pacotes exigidos: rvest
## Carregando pacotes exigidos: dplyr
##
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
##
## filter, lag
## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
##
## Carregando pacotes exigidos: tidyverse
## -- Attaching packages --------------------------------------- tidyverse 1.3.2 --
## v ggplot2 3.3.6 v purrr 0.3.4
## v tibble 3.1.8 v stringr 1.4.0
## v tidyr 1.2.0 v forcats 0.5.2
## v readr 2.1.2
## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x readr::guess_encoding() masks rvest::guess_encoding()
## x dplyr::lag() masks stats::lag()
## Carregando pacotes exigidos: fPortfolio
##
## Carregando pacotes exigidos: timeDate
##
## Carregando pacotes exigidos: timeSeries
##
## Carregando pacotes exigidos: fBasics
##
## Carregando pacotes exigidos: fAssetsFeito isto, o próximo passo é definir o horizote de tempo em que a análise será exeutada, isto é, o tempo de dispersão dos dados sobre o qual os riscos e possíveis retornos serão calculados. Especificamente, este documento optará por escolher um intervalo desde janeiro de 2015 até a data atual, optando por uma periodicidade semanal.
first.date <- as.Date('2015-01-01')
last.date <- Sys.Date()
freq.data <- 'weekly'O próximo passo é identificar os códigos de negociação das empresas na bolsa de valores e fazer o download das cotações no período escolhido. Neste caso, é preciso que os códigos de negociação sejam sucedidos da sígla “.SA”.
tickers <- c('SUZB3.SA','VALE3.SA','VIVT3.SA','MRFG3.SA')
l.out <- BatchGetSymbols(tickers = tickers,
first.date = first.date,
last.date = last.date,
freq.data = freq.data,
cache.folder = file.path(tempdir(), 'BGS_Cache'))
## Warning: `BatchGetSymbols()` was deprecated in BatchGetSymbols 2.6.4.
## Please use `yfR::yf_get()` instead.
## 2022-05-01: Package BatchGetSymbols will soon be replaced by yfR.
## More details about the change is available at github <<www.github.com/msperlin/yfR>
## You can install yfR by executing:
##
## remotes::install_github('msperlin/yfR')
##
## Running BatchGetSymbols for:
## tickers =SUZB3.SA, VALE3.SA, VIVT3.SA, MRFG3.SA
## Downloading data for benchmark ticker
## ^GSPC | yahoo (1|1) | Not Cached | Saving cache
## SUZB3.SA | yahoo (1|4) | Not Cached | Saving cache - Got 96% of valid prices | Got it!
## VALE3.SA | yahoo (2|4) | Not Cached | Saving cache - Got 96% of valid prices | Well done!
## VIVT3.SA | yahoo (3|4) | Not Cached | Saving cache - Got 96% of valid prices | Good stuff!
## MRFG3.SA | yahoo (4|4) | Not Cached | Saving cache - Got 96% of valid prices | Mas bah tche, que coisa linda!Agora é possível examinar o valor das cotações de cada empresa que compõe a carteira de investimentos.
ggplot(l.out$df.tickers, aes(x = ref.date, y = price.close)) +
geom_line() +
facet_wrap(~ticker, scales = 'free_y')+
theme_bw()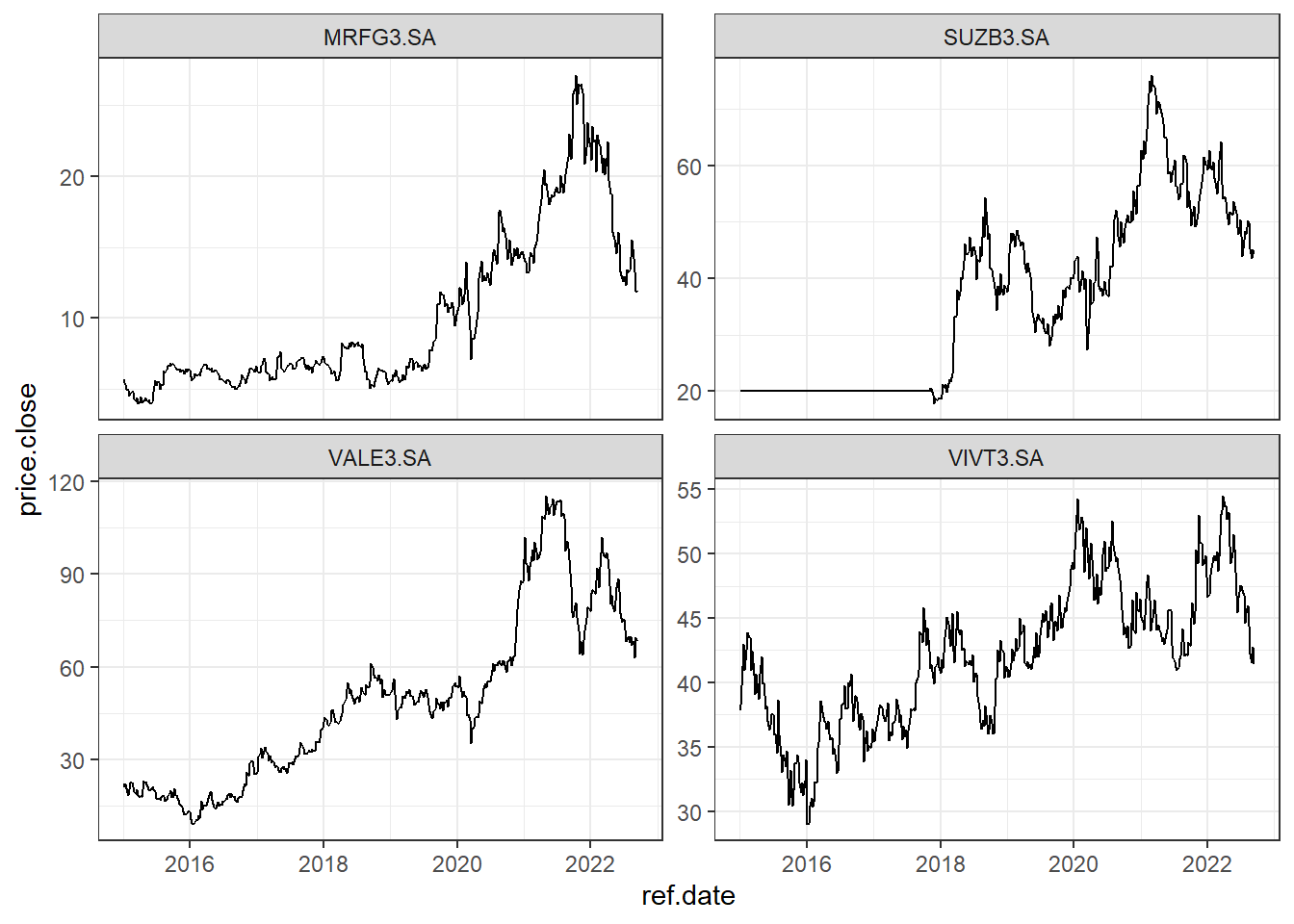
O próximo passo é montar uma matriz com as séries temporais de retornos obtidos na periodicidade escolhida (semanal).
suzano = l.out$df.tickers[l.out$df.tickers$ticker == "SUZB3.SA",] %>%
na.omit() %>%
select( ret.closing.prices) %>%
rename( Suzano = ret.closing.prices)
vale = l.out$df.tickers[l.out$df.tickers$ticker == "VALE3.SA",] %>%
na.omit() %>%
select( ret.closing.prices) %>%
rename( vale = ret.closing.prices)
vivo = l.out$df.tickers[l.out$df.tickers$ticker == "VIVT3.SA",] %>%
na.omit() %>%
select( ret.closing.prices) %>%
rename( Vivo = ret.closing.prices)
marfrig = l.out$df.tickers[l.out$df.tickers$ticker == "MRFG3.SA",] %>%
na.omit() %>%
select( ret.closing.prices) %>%
rename( Marfrig = ret.closing.prices)
retornos <- cbind(suzano, vale, vivo, marfrig)
retornos <- as.timeSeries(retornos)Tendo em mãos os retornos computados, o próximo passo é calcular os pesos de cada ativo na carteira ótima. A função tangencyPortfolio possibilita esse cálculo.
portfolio.eficiente <- tangencyPortfolio(retornos, spec = portfolioSpec(), constraints = "LongOnly")
portfolio.eficiente
##
## Title:
## MV Tangency Portfolio
## Estimator: covEstimator
## Solver: solveRquadprog
## Optimize: minRisk
## Constraints: LongOnly
##
## Portfolio Weights:
## Suzano vale Vivo Marfrig
## 0.3351 0.3368 0.0785 0.2495
##
## Covariance Risk Budgets:
## Suzano vale Vivo Marfrig
## 0.2911 0.4422 0.0174 0.2493
##
## Target Returns and Risks:
## mean Cov CVaR VaR
## 0.0037 0.0367 0.0746 0.0500
##
## Description:
## Wed Sep 14 09:33:09 2022 by user: helso
summary(portfolio.eficiente)
##
## Title:
## MV Tangency Portfolio
## Estimator: covEstimator
## Solver: solveRquadprog
## Optimize: minRisk
## Constraints: LongOnly
##
## Portfolio Weights:
## Suzano vale Vivo Marfrig
## 0.3351 0.3368 0.0785 0.2495
##
## Covariance Risk Budgets:
## Suzano vale Vivo Marfrig
## 0.2911 0.4422 0.0174 0.2493
##
## Target Returns and Risks:
## mean Cov CVaR VaR
## 0.0037 0.0367 0.0746 0.0500
##
## Description:
## Wed Sep 14 09:33:09 2022 by user: helso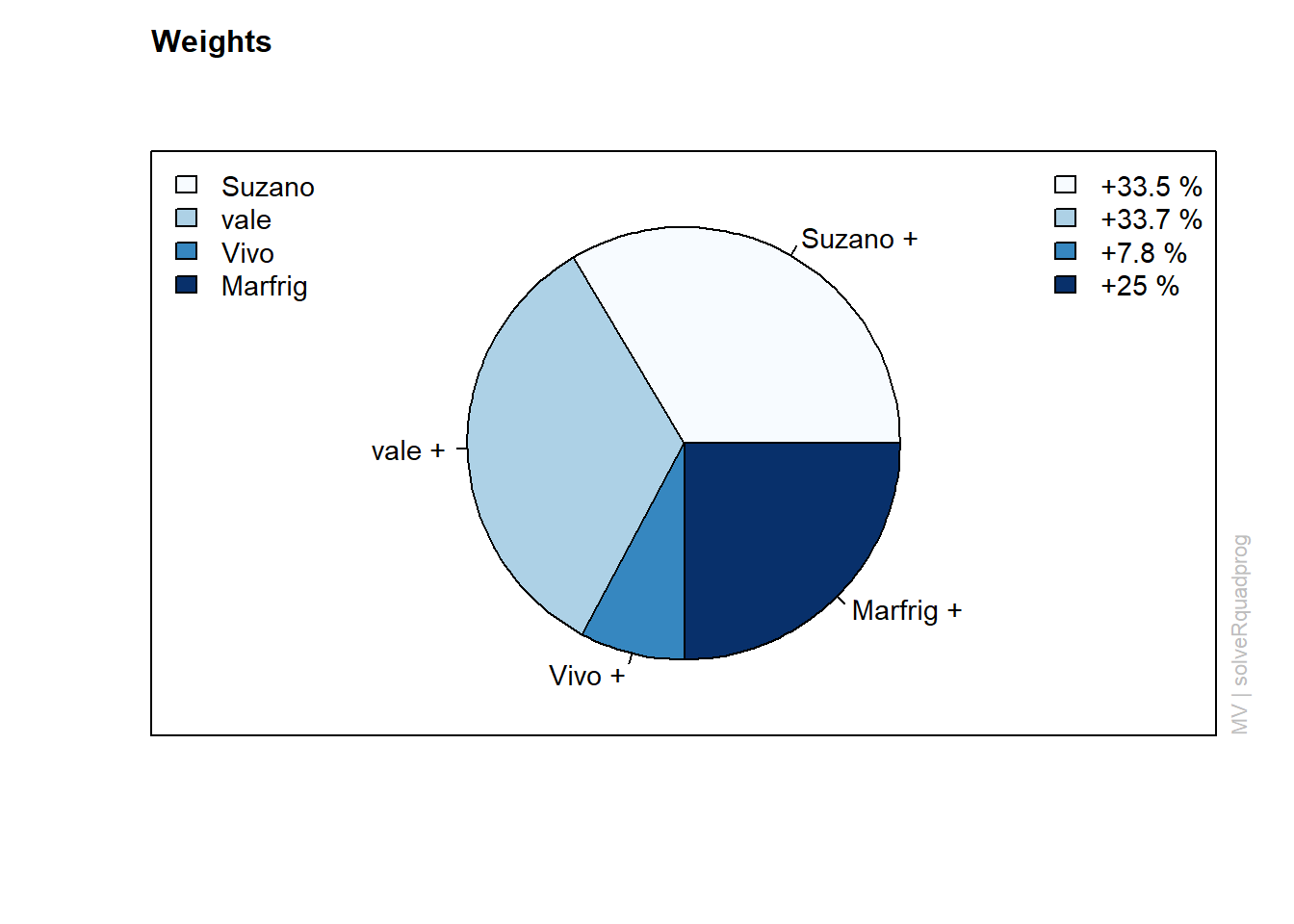
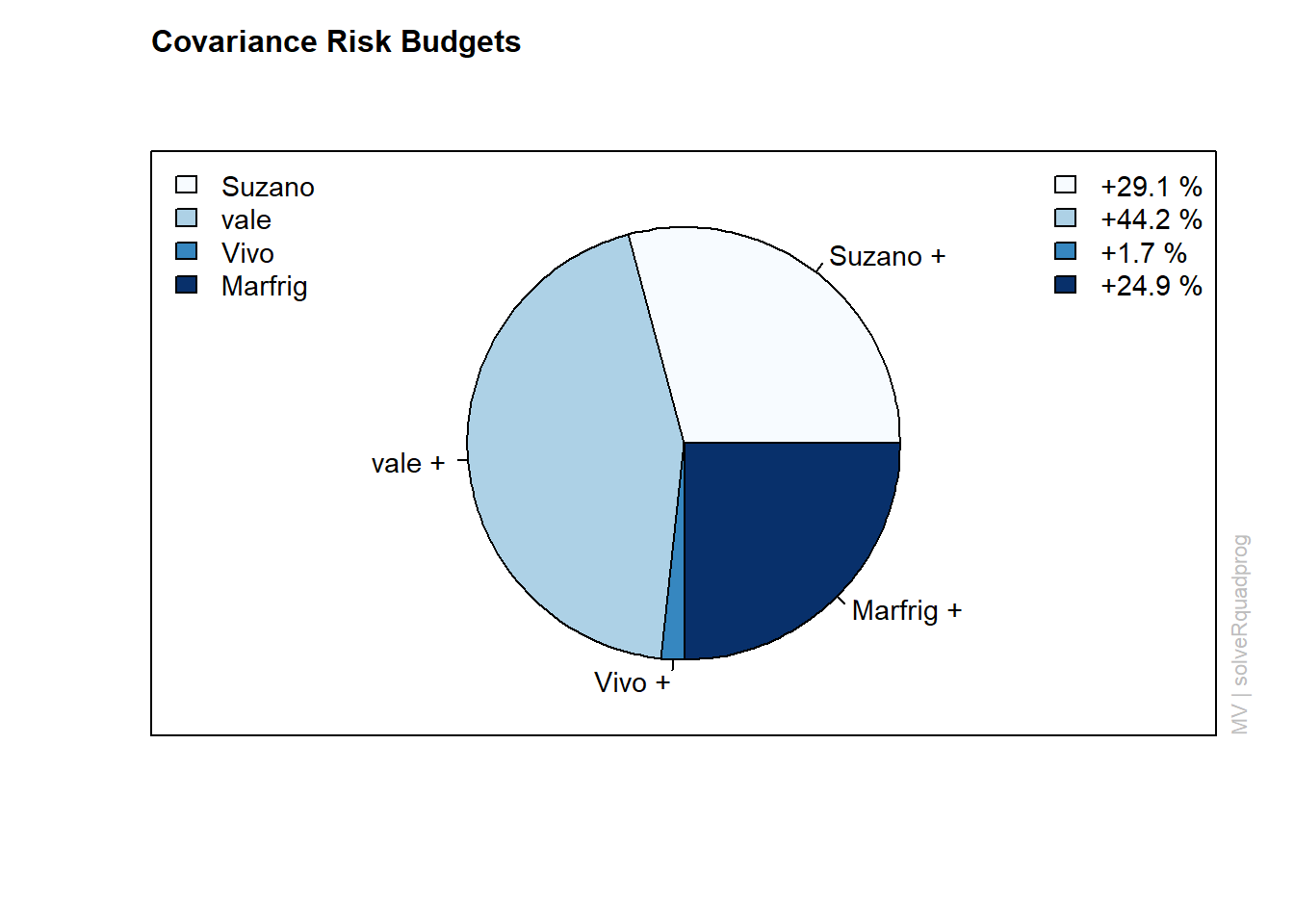
É possível notar que a carteira ótima deve denotar um maior peso (33,68%) para a empresa vale, enquato Suzano e Marfrig devem ter um peso de 33,51% e 24,95% na carteira, respectivamente.Nota-se facilmente que a empresa Telefônica possui o menor peso (7,85%), indicando que os riscos de investimento na Telefônica não são condizentes com o retorno esperado a esse nível de preços.
O próximo passo é elaborar a fronteira eficiente de Markowitz. A função portfolioFrontier possibilita a execução desta tarefa.
fronteira <- portfolioFrontier(retornos)
# Gráfico com a fronteira eficiente
frontierPlot(fronteira, col = c('blue', 'red'), pch = 20)
## Adicionando informações no gráfico
monteCarloPoints(fronteira, mcSteps = 5000, pch = 20, cex = 0.25 )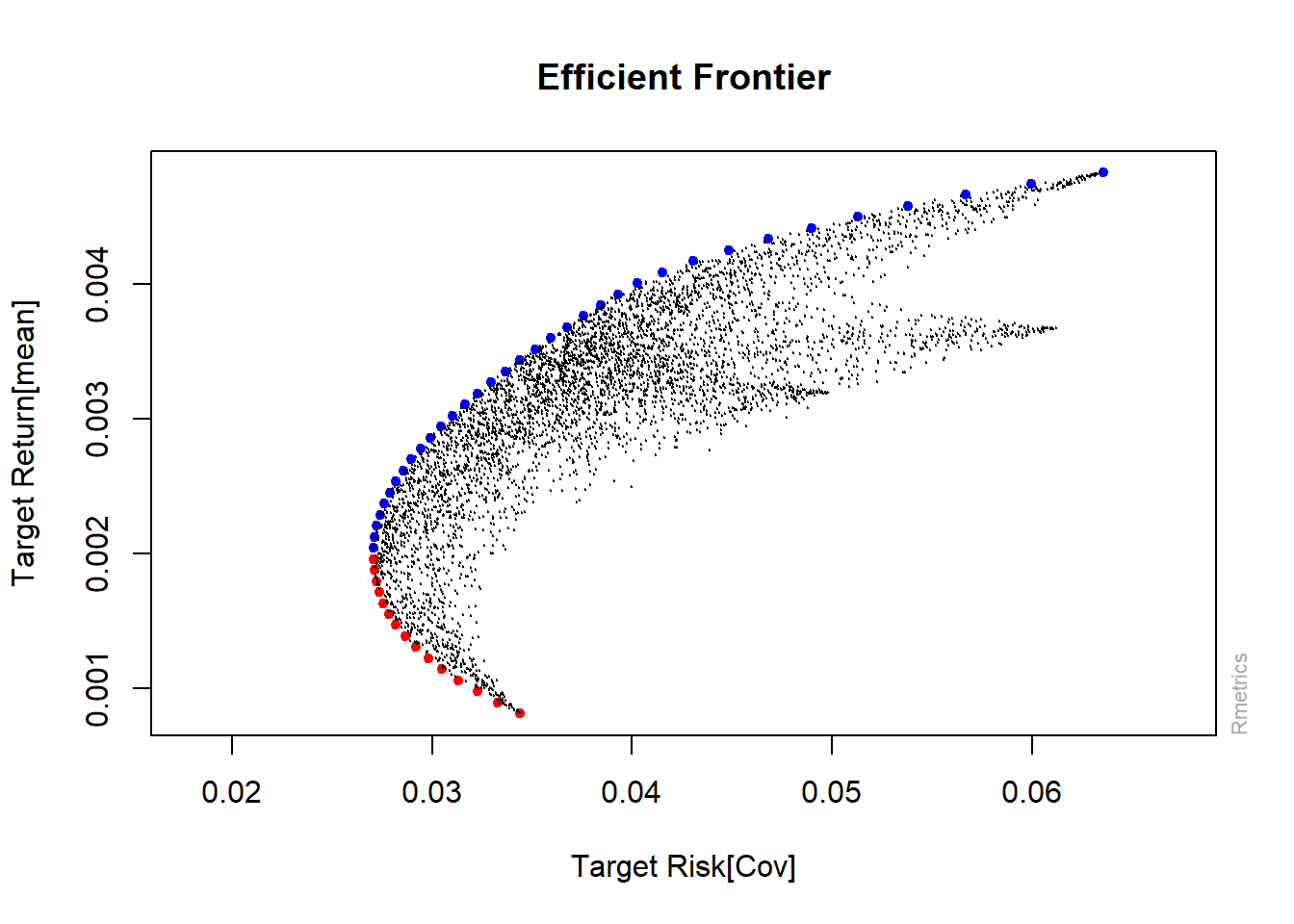
A fronteira ótima permite concluir que, se o agente é averso ao risco, então a sua posição comprada deve assumir um stop loss de cerca de 2,75% do valor investido, o que corresponde à exposição mínima ao risco indicada na fronteira. Em contrapartida, se o agente é propenso ao risco, então é possível estipular um stop loss de aproximadamente 6,25% da sua posição comprada, o que corresponde ao risco que atribuiria o maior retorno esperado da carteira.
