Escolha envolvendo risco: o caso da Mega-Sena
Introdução
Quando o consumidor faz uma escolha em um ambiente de risco, suas decisões são baseadas em uma utilidade esperada \(V\) para uma dada loteria. Supondo, por exemplo, uma loteria com três prêmios \(X = \{x_1, x_2, x_3\}\) e seja \(p_i\) com \(i = 1,2,3\) as probabilidades de obtenção destes prêmios, a utilidade esperada desta loteria pode ser medida como:
\[V = p_1 u(x_1) + p_2u(x_2) + p_3u(x_3)\]
Em que \(u\) é uma função que expressa a utilidade do prêmio em valores financeiros. Ao fazer uma escolha sobre loterias, o consumidor conhece o valor esperado de cada loteria \((\mathcal{V})\), o qual expressa a riqueza esperada com a aquisição da loteria e é dado por:
\[\mathcal{V} = p_1x_1 + p_2x_2 + p_3x_3\]
O caso da Mega-Sena
No caso da Mega-sena, o valor esperado do prêmio pode ser escrito como a diferença entre os produtos da probabilidade de acerto das seis dezenas com o valor do prêmio e do valor da aposta com a probabilidade complementar do acerto. No caso de uma aposta simples de seis dezenas, que custa R$ 4,50, este valor esperado pode ser escrito como:
\[\mathcal{V}_6 = p_{a,6}*x + (1-p_{a,6})(-P_6)\]
Em que \(\mathcal{V}_6\) reflete o valor esperado da aposta de seis dezenas, \(p_{a,6}\) é a probabilidade de acerto das seis dezenas com a aposta simples, e \(P_6\) é o preço da aposta simples (4,50). Como as apostas podem ter entre 6 e 20 números, a equação do valor esperado pode ser reescrita como:
\[\mathcal{V}_i = p_{a,i}*x + (1-p_{a,i})(-P_i) \quad \text{ Com } \quad i = {6, 7,...,20}\]
Para mensurar este valor esperado, considere usar a linguagem R e especificar os preços e as probabilidades referentes a cada aposta disponíveis no site da caixa [https://loterias.caixa.gov.br/Paginas/Mega-Sena.aspx]:
# probabilidades de acerto das
p6 = 1/50063860
p7 = 1/7151980
p8 = 1/1787995
p9 = 1/595998
p10 = 1/238399
p11 = 1/108363
p12 = 1/54182
p13 = 1/29175
p14 = 1/16671
p15 = 1/10003
p20 = 1/1292
# Valor das apostas
v6 = 4.5
v7 = 31.5
v8 = 126
v9 = 378
v10 = 945
v11 = 2079
v12 = 4158
v13 = 7722
v14 = 13513.5
v15 = 22522.5
v20 = 174420Considere instalar e liberar as bibliotecas necessárias para a análise:
lapply(list("dplyr", "tidyr", "ggplot2", "stringr", "rjson"), function(x){
if(x %in% installed.packages() == F){
install.packages(x)
library(x, character.only = TRUE)
}else{
library(x, character.only = TRUE)
}
})
FALSE
FALSE Attaching package: 'dplyr'
FALSE The following objects are masked from 'package:stats':
FALSE
FALSE filter, lag
FALSE The following objects are masked from 'package:base':
FALSE
FALSE intersect, setdiff, setequal, union
FALSE [[1]]
FALSE [1] "dplyr" "stats" "graphics" "grDevices" "utils" "datasets"
FALSE [7] "methods" "base"
FALSE
FALSE [[2]]
FALSE [1] "tidyr" "dplyr" "stats" "graphics" "grDevices" "utils"
FALSE [7] "datasets" "methods" "base"
FALSE
FALSE [[3]]
FALSE [1] "ggplot2" "tidyr" "dplyr" "stats" "graphics" "grDevices"
FALSE [7] "utils" "datasets" "methods" "base"
FALSE
FALSE [[4]]
FALSE [1] "stringr" "ggplot2" "tidyr" "dplyr" "stats" "graphics"
FALSE [7] "grDevices" "utils" "datasets" "methods" "base"
FALSE
FALSE [[5]]
FALSE [1] "rjson" "stringr" "ggplot2" "tidyr" "dplyr" "stats"
FALSE [7] "graphics" "grDevices" "utils" "datasets" "methods" "base"Agora considere extrair os valores dos prêmios da Mega-Sena a partir de uma api de dados disponibilizada gratuitamente. Para os devidos fins, considere obter os dados disponíveis na api desde o sorteio de número 1500 até o sorteio de número 2500, conforme o código abaixo:
# premios = data.frame()
#
# for(i in 1500:2565){
# link = sprintf("https://loteriascaixa-api.herokuapp.com/api/mega-sena/%i", i)
# df = fromJSON(file = link)
# df1 = as.data.frame(df$premiacoes[[1]])
# while (str_detect(df1$premio, "\\.") == T) {
# df1$premio = str_replace(df1$premio,'\\.', "")
# }
# df1$premio = str_replace(df1$premio,',', ".")
# df2 = data.frame(sorteio = df$concurso, premio = as.numeric(df1$premio))
# premios = rbind(premios, df2)
# rm(link, df, df1, df2)
# }Agora considere calcular o valor esperado para cada possibilidade de dezenas na aposta conforme o código a seguir:
premios = premios |>
na.omit()|>
mutate(
ve6 = p6*premio + (1-p6)*(-v6),
ve7 = p7*premio + (1-p7)*(-v7),
ve8 = p8*premio + (1-p8)*(-v8),
ve9 = p9*premio + (1-p9)*(-v9),
ve10 = p10*premio + (1-p10)*(-v10),
ve11 = p11*premio + (1-p11)*(-v11),
ve12 = p12*premio + (1-p12)*(-v12),
ve13 = p13*premio + (1-p13)*(-v13),
ve14 = p14*premio + (1-p14)*(-v14),
ve15 = p15*premio + (1-p15)*(-v15),
ve20 = p20*premio + (1-p20)*(-v20))O próximo passo é plotar os valores esperados e comparar os resultados para cada aposta. Para facilitar a visualização e reduzir os prejuízos visuais da escala, o código abaixo considera os valores esperados das apostas com 6, 7, 8 e 10 dezenas para cada sorteio contido no banco de dados.
Repare que o valor esperado é tão menor quanto maior for o número de dezenas que compõem a aposta. Repare também que na grande maioria das vezes o valor esperado da aposta é negativo, isto é, a expectativa predominante é de perder o valor gasto para realizar a aposta. Isto acontece porque o valor necessário para realizar uma aposta com mais números é grande o suficiente para contrabalancear os ganhos de probabilidade de acertar as dezenas sorteadas.
Note que a aposta mínima de seis dezenas é aquela em que o valor esperado torna-se positivo em uma maior frequência. Estes casos ocorrem quando o valor do prêmio é suficientemente grande para conpensar a elevada probabilidade de não acertar as dezenas sorteadas. Com isso, desconsiderando a utilidade dos prêmios, se você é um consumidor fracamente propenso ao risco, então o ideal seria realizar a aposta simples de seis números.
ggplot(data = premios) +
geom_line(aes(x = sorteio, y = ve6, color = "6 dezenas"), size = 0.8)+
geom_line(aes(x = sorteio, y = ve7, color = "7 dezenas"), size = 0.8)+
geom_line(aes(x = sorteio, y = ve8, color = "8 dezenas"), size = 0.8)+
geom_line(aes(x = sorteio, y = ve10, color = "10 dezenas"), size = 0.8) +
theme_bw() +
theme(legend.position = "bottom", legend.title = element_blank(), legend.text = element_text(size = 17)) +
xlab("Número do sorteio") + ylab("Valor esperado") +
scale_fill_discrete(breaks=c('6 dezenas', '7 dezenas', '8 dezenas', "10 dezenas"))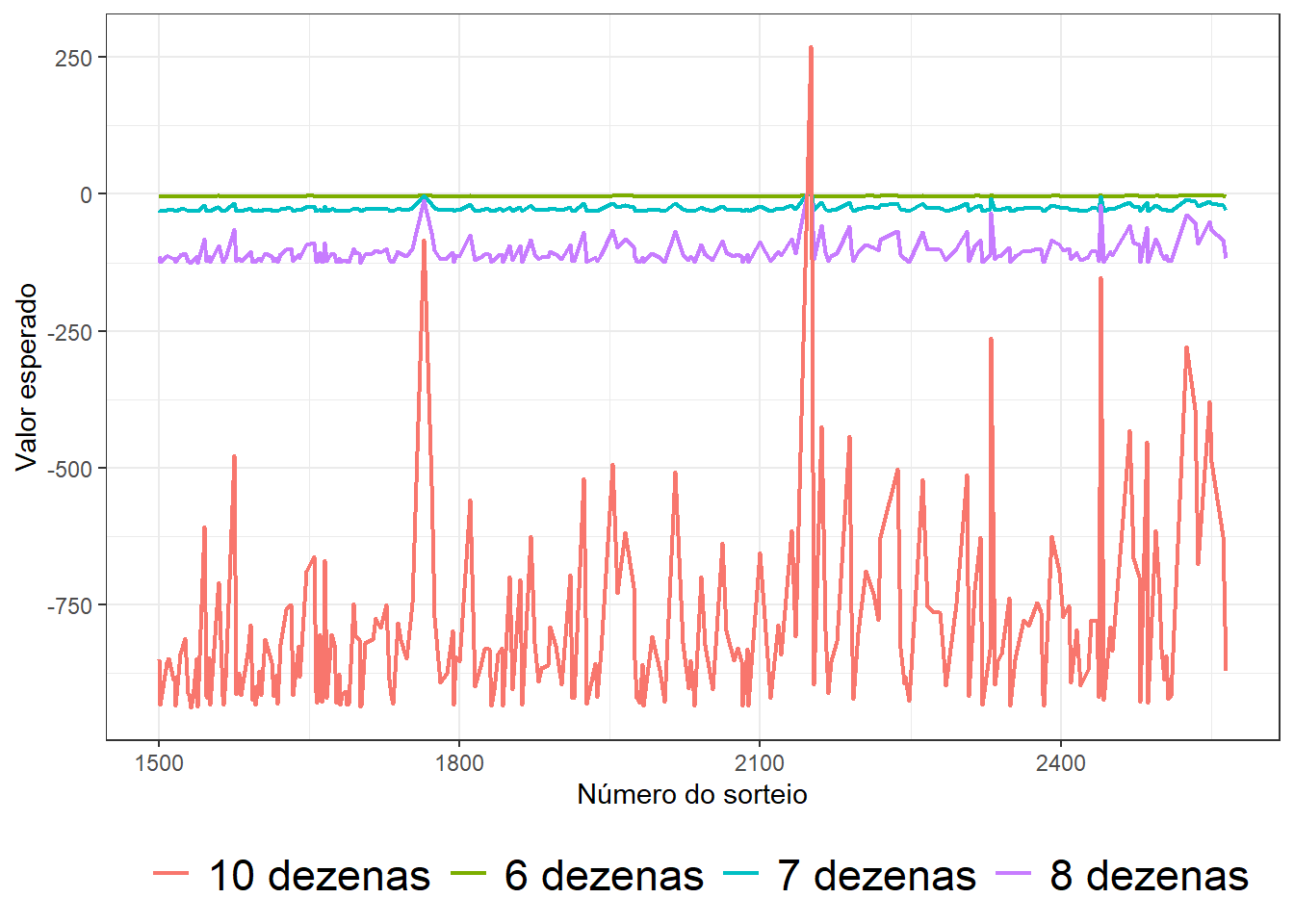
É importante destacar que do ponto de vista de um consumidor racional, a aposta torna-se atrativa apenas quando o valor esperado é superior ao montante gasto para realizar a aposta. Com isso, a Mega-Sena é racionalmente atrativa caso ocorra:
\[ p_{a,i}*x + (1-p_{a,i})(-P_i) > 0\] \[ p_{a,i}*x > P_i(1-p_{a,i})\] \[ x >P_i \left(\frac{1-p_{a,i}}{p_{a,i}} \right)\]
Calculando estes valores obtém-se que:
dt = data.frame(
Dezenas = c(6:15, 20),
probabilidade = c(1/5006860, 1/7151980, 1/1787995,
1/595998, 1/238399, 1/108363, 1/54182,
1/29175, 1/16671, 1/10003, 1/1292),
preco = c(
4.5, 31.5, 126, 378, 945, 2079,
4158, 7722, 13513.5, 22522.5, 174420
)
)
dt = dt|>
mutate(premio = preco*((1-probabilidade)/probabilidade))
print(dt[,c(1,4)])
FALSE Dezenas premio
FALSE 1 6 22530866
FALSE 2 7 225287339
FALSE 3 8 225287244
FALSE 4 9 225286866
FALSE 5 10 225286110
FALSE 6 11 225284598
FALSE 7 12 225284598
FALSE 8 13 225281628
FALSE 9 14 225270045
FALSE 10 15 225270045
FALSE 11 20 225176220Em que a terceira coluna mostra o prêmio mínimo necessário para tornar a aposta racionalmente atrativa. Entretanto, é válido ressaltar que estas análises são baseadas apenas no valor esperado do prêmio, e que uma análise mais confiável deve levar em consideração a utilidade esperada dos jogadores.
A teoria da escolha envolvendo risco postula que um consumidor averso ao risco possui uma função de utilidade convexa para os prêmios, enquanto o consumidor propenso ao risco possui funções de utilidade côncavas. Suponha, portanto, que o apostador mediano da Mega-Sena possui uma função de utilidade equivalente a \(u(x) = x^{x/a}\), em que \(a\) é um fator de desconto. Por simplicidade, considere \(a = 200.000.000\), o que torna \(u(x)\) uma função convexa que representa um consumidor propenso ao risco. Assim, a utilidade esperada da aposta é:
\[V_i = p_{a,i}*x^{x/a} + (1-p_{a,i})*(-P_i)^{-P_i/a} \quad \text{ Com } \quad i = {6, 7,...,20}\]
Calculando a utilidade média esperada para cada prêmio, obtém-se:
a = 200000000
premios |>
group_by()|>
summarise(
ue6dezenas = mean(p6*(premio^(premio/a)) + (1-p6)*(-v6^(-v6/a))),
ue7dezenas = mean(p7*(premio^(premio/a)) + (1-p7)*(-v7^(-v7/a))),
ue8dezenas = mean(p8*(premio^(premio/a)) + (1-p8)*(-v8^(-v8/a))),
ue9dezenas = mean(p9*(premio^(premio/a)) + (1-p9)*(-v9^(-v9/a))),
ue10dezenas = mean(p10*(premio^(premio/a)) + (1-p10)*(-v10^(-v10/a)))
)
FALSE # A tibble: 1 x 5
FALSE ue6dezenas ue7dezenas ue8dezenas ue9dezenas ue10dezenas
FALSE <dbl> <dbl> <dbl> <dbl> <dbl>
FALSE 1 143. 1010. 4043. 12132. 30332.Note que conforme o número de dezenas na aposta aumenta a utilidade esperada do apostador mediano cresce, o que se verifica para quaisquer funções de utilidade convexas bem comportadas. Este resultado decorre do fato de que embora o valor da aposta aumente, o ganho de utilidade para a expectativa de acertar a aposta supera o ganho de desutilidade de não acertar as dezenas e consequentemente perder o valor gasto na aposta. O contrário é válido para um consumidor averso ao risco com função de utilidade côncava.
Conclusão
Caso o consumidor tome suas decisões com base apenasno valor esperado da Mega-Sena, então o ideal é realizar uma aposta simples de 6 dezenas. Se o consumidor é averso ao risco, mas mesmo assim deseja realizar uma aposta, então é esperado que ele também opte pela aposta simples. No entanto, um consumidor propenso ao risco que toma as suas decisões com base na utilidade esperada do prêmio sempre estará disposto a realizar uma aposta com mais dezenas.
